Történt egyszer, hogy rábukkantam egy remek blogbejegyzésre, ami azt feszegette, milyen esélyek vannak a Malifaux-ban, ha például 9-et akarunk húzni [-] flippel. Sajnos a blogíró ennél tovább nem nagyon ment, így kénytelen voltam Excelbe önteni az alapadatokat, hogy azokból néhány érdekesnek vélt grafikont itt is megosszak a közepesen alacsony számú olvasói táborral.
Szóval a kiindulás ez a táblázat, amiből leolvasható, hogy ha minimum X-et kell egy próbán elérnünk, arra mennyi esélyünk lesz. (Természetesen teljes paklit feltételezve, ami egy kényszerű egyszerűsítés.)
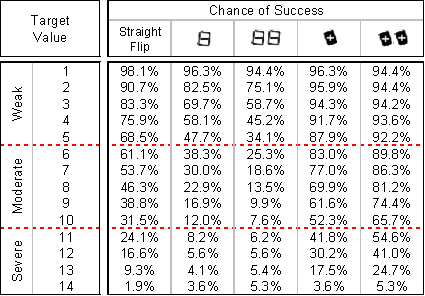
Mint az látható, [-][-] flipre ugyanannyi esélyünk van 14-et elérni, mint [+][+]-szal. Ez egyike a tipikus malifaux-s specialitásoknak. A dzsókerek ugyanis teljesen megbolondítják az ilyen jellegű valószínűségi táblázatok legalsó és legfelső traktusát. A táblázaton érdemes kicsit elmélázni, mert a kártyarendszer számos finomságára rávilágít.
Arra viszont ez a számhalmaz ebben a formában nem alkalmas, hogy például megtudjuk, Cb5-tel és [+] flippel támadva egy Df7-es sima flippel védekező modellt, mennyi esélyünk van arra, hogy ellenfelünknek kelljen kezdenie a csalást (azaz neki kisebb Starting Total jöjjön ki). Az ilyen és ehhez hasonló kérdések megválaszolására a külhoni kolléga számait szétszedtem, majd saját táblázatokba öntöttem. Ezek viszont nem annyira könnyen befogadhatók, mint mondjuk a Bors címlapja. Így inkább csináltam belőlük grafikonokat, hátha akkor azok is hajlandóak lesznek belenézni, akiknek az Excel szó hallatán ökölbe szorul az arcuk.
Első ábránk egy roppant egyszerű kérdésre ad választ: mennyi a várható értéke egy húzásnak?
Várható érték különböző fliptípusoknál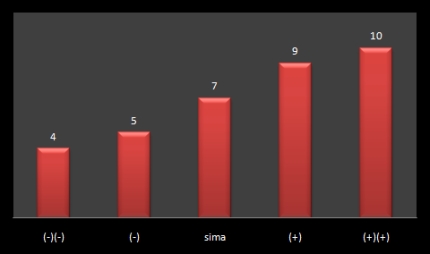
Ahogy az várható (muhahaha) volt, a sima flipnél 7 lesz az eredmény, hiszen 1-től 13-ig egyenlő számú kártyából húzunk (és ezt a nullát érő Black Joker és a 14-es Red sem borítja fel). Az viszont már a csatatéren konkrétan felhasználható tudás, hogy tisztában vagyunk vele (körülbelül) 2-vel nagyobb karakterisztikával lehet az ellenfél [+] flipjét kiegyenlíteni egy képességpróbás párharc során. Szintén érdekes megfigyelni, hogy az első plusz (vagy mínusz) kártya 2-vel módosítja a várható értéket, de a második már csak 1-gyel.
Sima flip esélye [+]/[-] flipek és eltérő karakterisztikák ellen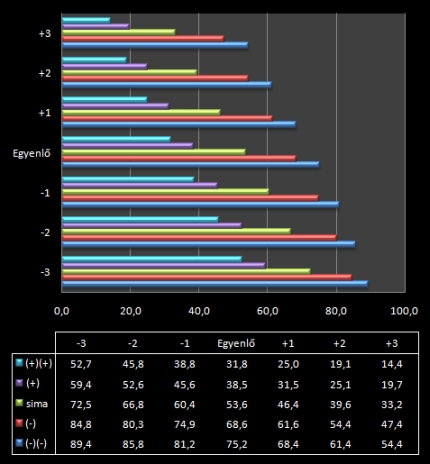
Az elsőre talán kicsit sok dolgot tartalmazó második ábránkból szinte bármilyen alapvető duelnél megnézhetjük azt, mennyi az esélyünk a csalások megkezdése előtt az ellenfelünknél jobb értéket elérni. A flipek ellenfelünk húzására vonatkoznak, a számok pedig arra, mennyivel kell jobb, vagy rosszabb számszerű eredmény a sikerünkhöz (magyarul, kinek van jobb alapstatisztikája és kinek kedvez a döntetlen).
Példa: Wp->Wp Duelt kell tennünk. Nekünk Wp6 van, ellenfélnek Wp5, ráadásul még [-] flipet is kap rá. A döntetetlen nekünk elég, ezért a kérdéses százalékot a -1 oszlopból nézzük ki (mivel eggyel jobb a Wp-nk). A sor a [-] flip kezdetű, hiszen ennyivel húz az ellenfél. Megkapjuk, hogy 74,9. Azaz ha eggyel jobbak vagyunk és az ellenfél még negatív flipben is van, akkor 4 Starting Duelből átlag 3-ban mi leszünk a jobbak. Ráadásul itt speciel már csalni sem lehet az ellenfélnek.
A táblázatból olyan esetekre is tudunk százalékot mondani, amikor mi nem sima flippel megyünk (viszont az ellenfél igen). Ilyenkor szimplán csavarni kell egyet a gondolatmeneten.
Fordított példa: Cb4-gyel, de Paired fegyverrel csapnánk oda egy Df7-es ellenfélnek. Az esélyt ilyenkor úgy kapjuk meg, hogy ellenfelünk szemszögéből nézzük meg a táblázatot (majd a kapott eredményt kivonjuk a 100%-ból). Tehát Df7-tel Cb4 ellen maximum 2-vel kisebb lap húzásánál is sikerül védeni a támadást. Azaz a -2 oszlopot kell nézni, és természetesen a [+] flipes sort, mivel a támadónak Paired fegyvere van. Itt 52,6% van, ami azt jelenti, hogy támadóként 47,4% esélyünk van a jobb kezdésre a Duelben.
Különböző méretű sebzések esélye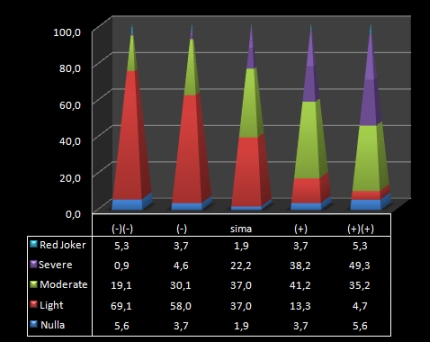
Ha már sikerült találnunk, érdemes megnézni, mennyit tudunk sebezni. A fenti oszlopok szép színekkel mutatják, milyen flipnél mekkora eséllyel fogunk kicsi/közepes/nagy sebzésértéket kapni. Ez szerintem magyarázat nélkül is teljesen érthető, de azért az például érdekes, hogy [+][+]-nál is 50 százaléknál alig valamivel több (49,3+5,3) esély van a naon dulva sebzésre.
Sebzéspontok várható értéke eltérő fegyvereknél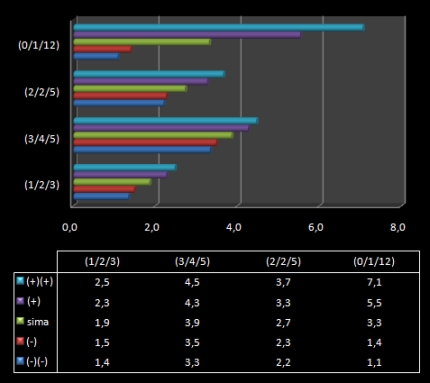
Végül csináltam pár példát arra, hogy az eltérő sebzéskódok miként befolyásolják a ténylegesen beadott Damage értékét. Itt jól látszik, hogy kiegyensúlyozott felállásban (3/4/5) általában nem érdemes nagy áldozatokat hozni azért, hogy egy [+] flipet összekaparjunk, vagy egy [-]-t eltüntessünk (természetesen a csalhatunk - nem csalhatunk kérdésen kívül). Ugyanakkor Leveticusnál apait-anyait bele kell tolni, mert a két szélsőérték között 6,5-szeres különbséget találunk.
Ezek csak gondolatébresztő példák akartak lenni, remélem mindenki talál benne valami érdekességet, amit aztán a gyakorlatban is tud kamatoztatni.
Disclaimer: az elmondottaknál az egyszerűség kedvéért nem vettem figyelembe azokat az eseteket, amikor egyik vagy másik dzsókert nem lehet már felhúzni, vagy például azt sem, hogy mennyire forró egy pakli, azaz milyen értékű lapok mentek már ki.











![Guild Ball: Masons vs. Butchers ligadöntő [videó]](https://m.blog.hu/ge/geistwald/image/.external/.thumbs/dc67137bc983049f109cc5d291d8e357_669ba6b3c379af695492e9efd7630b86.jpg)
![Guild Ball: Union vs. Fisherman [videó]](https://m.blog.hu/ge/geistwald/image/.external/.thumbs/385313662cc6b412962203de6a406be3_669ba6b3c379af695492e9efd7630b86.jpg)
