Történt egyszer, hogy rábukkantam egy remek blogbejegyzésre, ami azt feszegette, milyen esélyek vannak a Malifaux-ban, ha például 9-et akarunk húzni [-] flippel. Sajnos a blogíró ennél tovább nem nagyon ment, így kénytelen voltam Excelbe önteni az alapadatokat, hogy azokból néhány érdekesnek vélt grafikont itt is megosszak a közepesen alacsony számú olvasói táborral.
Szóval a kiindulás ez a táblázat, amiből leolvasható, hogy ha minimum X-et kell egy próbán elérnünk, arra mennyi esélyünk lesz. (Természetesen teljes paklit feltételezve, ami egy kényszerű egyszerűsítés.)
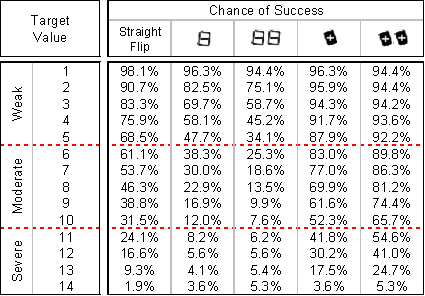
Mint az látható, [-][-] flipre ugyanannyi esélyünk van 14-et elérni, mint [+][+]-szal. Ez egyike a tipikus malifaux-s specialitásoknak. A dzsókerek ugyanis teljesen megbolondítják az ilyen jellegű valószínűségi táblázatok legalsó és legfelső traktusát. A táblázaton érdemes kicsit elmélázni, mert a kártyarendszer számos finomságára rávilágít.
Arra viszont ez a számhalmaz ebben a formában nem alkalmas, hogy például megtudjuk, Cb5-tel és [+] flippel támadva egy Df7-es sima flippel védekező modellt, mennyi esélyünk van arra, hogy ellenfelünknek kelljen kezdenie a csalást (azaz neki kisebb Starting Total jöjjön ki). Az ilyen és ehhez hasonló kérdések megválaszolására a külhoni kolléga számait szétszedtem, majd saját táblázatokba öntöttem. Ezek viszont nem annyira könnyen befogadhatók, mint mondjuk a Bors címlapja. Így inkább csináltam belőlük grafikonokat, hátha akkor azok is hajlandóak lesznek belenézni, akiknek az Excel szó hallatán ökölbe szorul az arcuk.










